Many difficulties arise during the construction of a brick house, but they are all quite easily overcome. The most popular complication is attaching the rafters to a brick wall, since this surface requires the most sensitive attitude to itself.

The angle of assembly of the truss system depends on the slope of the roof slope.
Mauerlat and methods of its installation
Tools and materials:
- tape measure;
- bar 100 * 100;
- perforator;
- waterproofing;
- pins, steel rods or wooden wedges.
The whole scheme of fastening the structure can be seen in fig. 1:

Figure 1. The scheme of fastening the rafters to a brick wall: 1 - Tying; 2 - Mauerlat; 3 - Waterproofing; 4 - Rafters; 5 - Wire; 6 - Fixing anchor.
- Binding. This method of fastening is carried out most often, but there are exceptions for studs.
- Mauerlat.
- Waterproofing.
- Rafters.
- Wire.
- Locking anchor.
At the very beginning, you need to install the power plate, since the construction begins with it. Before its installation, cut brick is laid from the front side, in order to close it. Some masters put a brick after work, which is also effective, but takes a little longer. As a waterproofing, it is better to use penetrating options, but if there is no way to get them, or the price is too heavy, it is quite possible to do with roofing material. After the roofing felt is rolled at its location, you need to burn it with a gas torch.
There are 3 ways to attach the power plate:
- Stud. This method is the easiest, since you need to make a vertical hole in the wall to a depth of 1/2 of the stud, pour a little non-hardening mastic on the bottom and immerse a metal rod there. A bar is installed on top with holes made in the right places. The mounting pitch is usually 30-40 cm, since the increase will affect the strength properties.
- Wooden wedges. It's all much simpler, because when laying bricks left special gaps, which will be installed wedges of the desired length. It will just be necessary to make holes in the timber in the selected places with a drill and fasten them together. Wedges must be of coniferous wood or more expensive varieties, so that lasted as long as possible.
- Steel bars. The step of their installation is 30-40 cm, and the method is identical to wooden analogues. Such rods are much cheaper than wood, and their installation is simpler. The only drawback is the need to do the deepening of 3 rows of masonry so that the cracks from the roof do not go from the lateral pressure around the house (working with light materials does not require such precautions, but it is better to make sure).
Some craftsmen heat waterproofing to a viscous state before laying the mauerlat, thereby improving the hitch. Such a move is impossible when using mastics, since for them it is extremely destructive.
Basic installation work
Tools and materials:
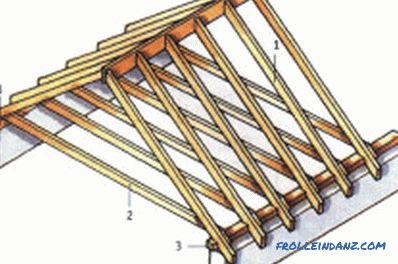
Gable roof construction: 1 - Rafters; 2 - Coupler; 3 -
Mauerlat; 4 - Ridge.
- bar 80 * 200;
- corner of steel;
- tape measure;
- circular saw;
- pencil and cardboard;
- wire;
- anchors;
- punch.
Now the installation of rafters on the walls begins. The rafter system depends on the type of roof chosen, but the most often used is a gable:
- Rafters.
- Coupler.
- Mauerlat.
- Ridge.
This option is quite simple to install, moreover, you will not need to make additional partitions under the roof. At the very beginning, beams are installed for the screed with a pitch of 0.8-1.2 m depending on the weight of roofing materials (for an ondulin or reed 1.2 m is enough for the eyes, whereas for slate - 0.8 m and not more). Fastening to the power plate is carried out with the help of special corners made of galvanized steel. Only now the wall is ready to begin mounting the rafters.
Their length is calculated in such a way that the wall does not limit their length, and the beam goes 50 cm beyond its limits. At the junction of the tree and the wall you need to cut out triangles that clearly follow the contours of the corner with which the joint goes. Here it is best to make a cardboard layout, which will be taken measure, and with the help of circulars to make cutting.
At the very beginning, 3 beams are seized between each other, with 2 guides, and 1 ridge. It is not necessary to grab the ridge beam immediately rigidly so as not to strain the material. Raise the need so that the corners are perfectly matched. After 1 side has been raised, it is necessary to lift the opposite side and only after that fix them tightly with steel corners.
Each raised beam is immediately wrapped with galvanized wire, after which the wire is interlaced and led down.At a distance of 5 rows of masonry, you need to make a hole with a perforator, then thread the wire onto the anchor and screw it in until it is fully fixed.
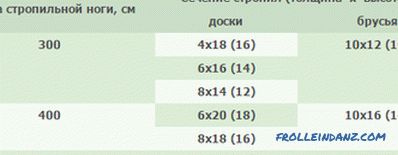
Dimensions of rafter legs.
The fixing of the rafters ends here, but a number of factors need to be remembered:
- When working with a punch, only drills and crown with a diamond bit are used. Any other options are more likely to split the material.
- All metal is strictly galvanized. If you mount the rafters on plain steel, then over time it will rust, and with it a tree will become worthless.
- All wood is carefully treated with an antiseptic against moisture and insects. Such a step will add up to 20 years of operational life.
Summing up
Before attaching the rafters with your own hands, you need to prepare yourself most thoroughly for this process. Wood is chosen mainly coniferous, galvanized metal, and the tool is reliable.
Usually, mounting the rafters on an area of 100 m² without assistants takes up to 1 week, so you need to preview the weather forecast in order not to fall under the rain.
If rains are foreseen, and the work must be carried out ahead of time, then during the precipitation the work is stopped and closed by polyethylene, and immediately after their completion, you can continue to work.
Didn't find the answer in the article? More information on the topic:
-
Features of the truss system
Endova rafter system: features of the device, the necessary materials and tools. Varieties rafters installation diagram. Step by step installation instructions do-it-yourself.
-
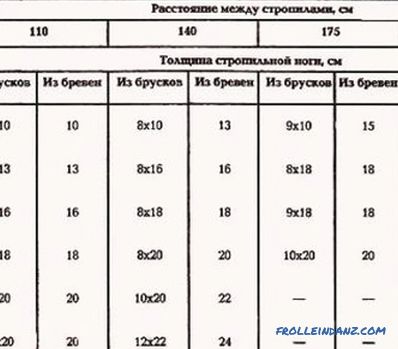
We make rafters for a two-slope roof
We make rafters for the roof with our own hands. Roof types and features of their construction. Materials required for arranging truss construction. The definition of the cross section of a bar or board.
-

How to mount a lag to a concrete floor?
Rigid lag attachment to the concrete floor with metal anchors. Technology mounted on the concrete frame of the adjustable lag. Lists of the necessary tools and materials.



